Simanaitis Says
On cars, old, new and future; science & technology; vintage airplanes, computer flight simulation of them; Sherlockiana; our English language; travel; and other stuff
MATHEMATICAL INDUCTION: DOMINOES OF LOGIC
THE WORD “INDUCTION” has a whole bunch of meanings: Merriam-Webster starts with “the act or process of inducting (as into office),” which is sort of a definitional cop-out: What’s “inducting”?
Another M-W citation is “a preface, prologue, or introductory scene especially of an early English play.” Interesting, but bordering on the theatrically obscure.
There’s also “the act of bringing forward or adducing something (such as facts or particulars).” This one includes electrical induction of magnetized bodies, the biologic fate of embryonic cells, and even the perhaps more familiar internal-combustion idea of fuel and air entering on the first of a four-stroke process.
M-W also cites “inference of a generalized conclusion from particular instances—compare DEDUCTION sense 2a.” What a good topic for another day! Which did Sherlock Holmes employ? Deduction? Induction? Both?
And, finally, there’s today’s topic here at SimanaitisSays: mathematical induction, the “demonstration of the validity of a law concerning all the positive integers by proving that it holds for the integer 1 and that if it holds for an arbitrarily chosen positive integer k, it must hold for the integer k+1.”
Here’s an example of mathematical induction, offered by comet.lehman.cuny.edu: Prove that 1+2+…+n = n(n+1)/2. For instance, 1+2+…+8 = 8×9/2= 72/2 = 36.
The First Domino. Verify the equation for n=1: Is 1 equal to [1x (1+1)]/2? Yep. The first domino is standing, ready to initiate the logic.
Lining Up the Other Dominoes. Assume for an arbitrary k that 1+2+… +k = k(k+1)/2. Prove that this implies the equation must work for k+1:
1+2+…+(k + 1) = (1+2+…+k)+(k+1) = [k(k+1)/2] + (k+1), this first bracketed part by the Induction Hypothesis. With some algebraic regrouping, = [k(k+1)+2(k+1)]/2 = [(k+2)(k+1)]/2, by factoring the (k+1)s, =[(k+1)(k+2)]/2, by the commutative nature of multiplication.
Thus, assuming the equation works for k implies it also works for k+1.

Image from abeon.hosting.
Loosely, the first domino is tipped, and the carefully aligned others all tumble.
Gauss’s Genius. There’s a charming story about the young Carl Friedrich Gauss, destined to be known as Princeps mathematicorum, loosely (and incorrectly) the Prince of Mathematicians.

Carl Friedrich Gauss, 1777–1855, German mathematician and physicist. In fact, Princeps mathematicorum is Latin for “the foremost of mathematicians.
His elementary school teacher tasked students to compute the sum 1+2+…+100. (Unlike us, they hadn’t covered math induction yet.) Gauss baffled the teacher by quickly saying “5050.”
Here’s how he did it:
Gauss recognized he had 50 pairs of numbers, each pair adding to 101. Thus, 50 x 101, or 5050. Easy-peasy.
This, gentle reader, is why Gauss was Princely. ds
© Dennis Simanaitis, SimanaitisSays.com, 2019


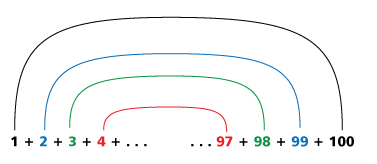
I figured this one out years ago myself, somewhat sure that I wasn’t the first to do so.
Also summing between two numbers, say n and m would be m*(m+1)/2-n*(n-1)/2. Example sum between 4 and 11: 11*12/2-4*3/2 = 66-6 = 60.
4+5+6+7+8+9+10+11 = 60