REULEAUX FUN: VENN ARRANGED JUST SO

A REULEAUX TRIANGLE, according to Wikipedia, is “a curved triangle with constant width, the simpliest and best known curve of constant width other than the circle.” By the way, it gets its name from Franz Reauleaux (“Ro-lo,”) a 19th-century German engineer who found its constant width helpful in his mechanical designs.

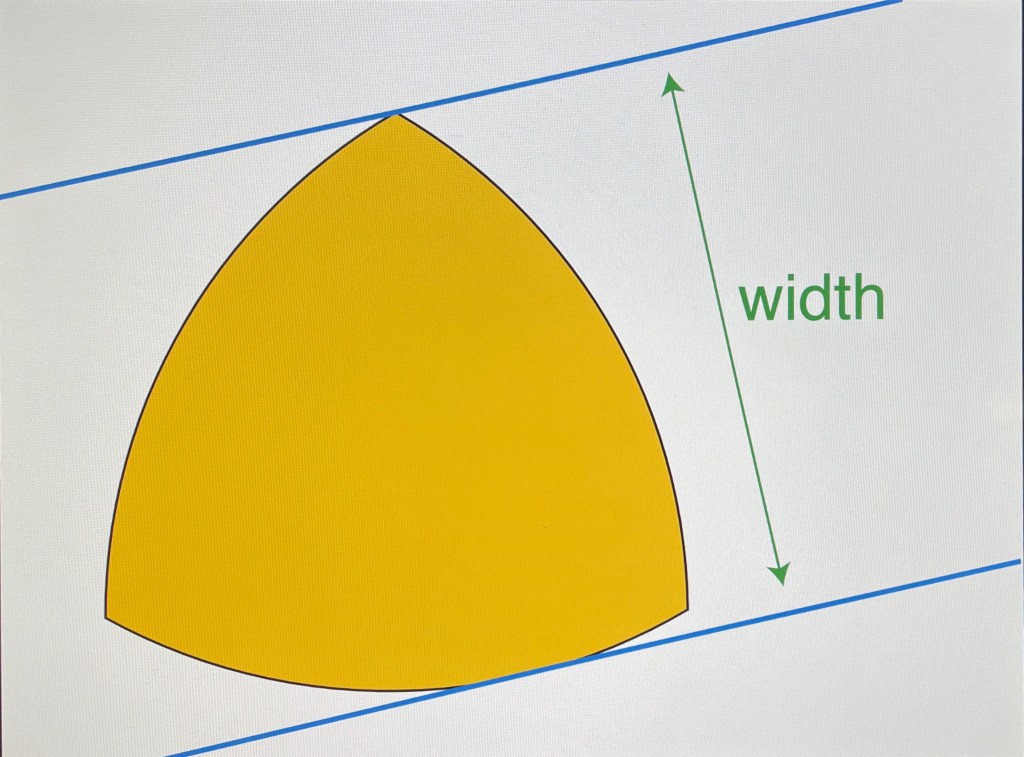
Reuleaux triangle. Note, each arc is equidistant from its opposite vertex. Image by David Eppstein from Wikipedia.

Rolling Jus’ Fine. A Reuleaux triangle’s constant width in any orientation implies it makes a perfectly useful three-sided “wheel.” There’s an oddity, though: A circular wheel has a unique point—its center—around which it rotates. By contrast, a Reuleaux triangle rotates around points forming a circle. 

One implication of this is the curious suspension of a Reuleaux bicycle. Its rider rolls along conventionally while its two axles follow their circular path.

See “Triangle Wheeled Bike—Burning Man 2012.” YouTube by Phillip Miller.

Drilling a Square Hole. Another implication of this odd rotation is the Reuleaux triangular drill bit—for square holes. 

See “How to Drill a Square Hole.” YouTube by Jill Britton.

What About a Higher-Dimensional Reuleaux Ball? Isaac Schlutz writes in Gizmodo, June 20, 2024, “Mathematicians Are Excited About a Newly Discovered Shape.”

“Now,” Schultz recounts, “a team of mathematicians say they’ve scaled up the shape into the third dimension and beyond, finding it resolves a math problem that’s been floundering since 1988. The original problem was put forth by Oded Schramm, a mathematician who considered whether objects of a constant width smaller than a sphere of a higher dimension might exist. The team’s research is currently hosted on the preprint server arXiv.”

Shultz shares: “The most amazing thing is that volume of each shape is easily computable,” said study co-author Andriy Bondarenko, a mathematician at the Norwegian University of Science and Technology, in an email to Gizmodo. “So we can compare n-volume of the shape with the n-volume of unit ball and see mathematically rigorously that volumes of our shapes are exponentially smaller.”

Beyond Three Dimensions. Pre-Einstein, mathematics had dimensionality by extending the number line to the plane (x,y), and then 3-space with (x,y,z). So why not 4-space (x,y,z,t) to describe the space/time continuum.

In the plane, the equation (x-h)² + (y-k)² = r² describes a circle (a “2-ball”) of radius r centered at point (h,k). In n-space, an n-ball of radius r centered at the origin would be defined by n of the terms x² + y² + …. w² = r².

3-D and Beyond. “In two dimensions,” Shultz observes,  the shape is a Reuleaux triangle. Seen in three-dimensional space, the shape is oblong, but something our brains can visualize. Beyond the third dimension, the team can mathematically project the shape’s constant width even in increasing dimensions.

A 3-D analog still rolls as shown here.

Constructing a 2-D Reuleaux Triangle—Venn You Like. It’s good fun constructing a Reuleaux triangle using whatever graphical software you possess. Being the Luddite I am, I use ancient Jasc Paint Shop Pro 6.0, which works fine with my equally classic GMax and Microsoft FS-9.

An Equilateral Start. It begins with constructing an equilateral triangle. Here’s the sequence:  

A triangle base.

 A circle centered at one end passing through the other.

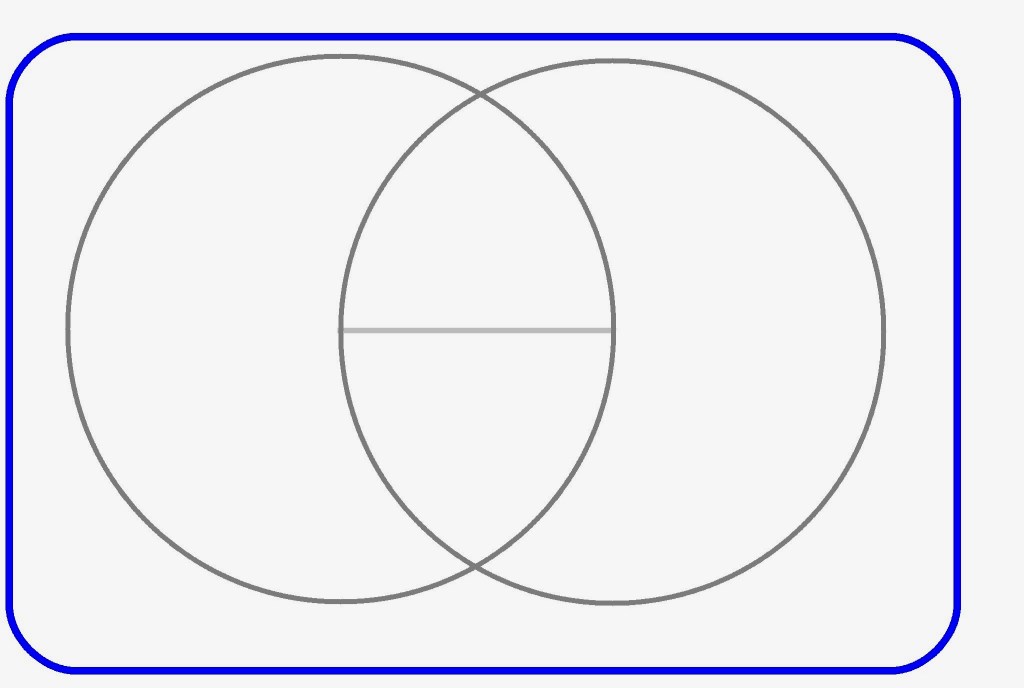
Another circle of the same size centered at the other end.

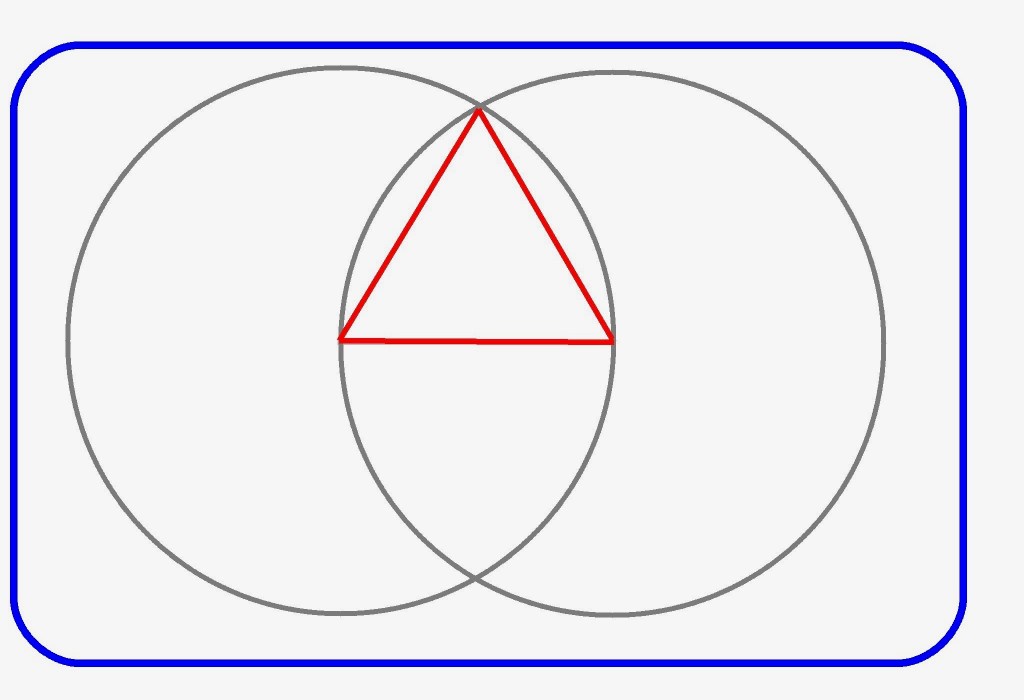
Construct the other two sides to complete the equilateral triangle.

A Quick Reuleaux Triangle. Center a third circle of the same size at the tip of the equilateral triangle. The intersection of the three circles forms a Reuleaux triangle. Think of it as a bloated equilateral triangle, but bloated precisely enough.

Venn You Have Time. There’s a completely different interpretation of the final step: It’s a Venn diagram, using overlapping circles that describe three populations each of which shares a specific commonality with the other.

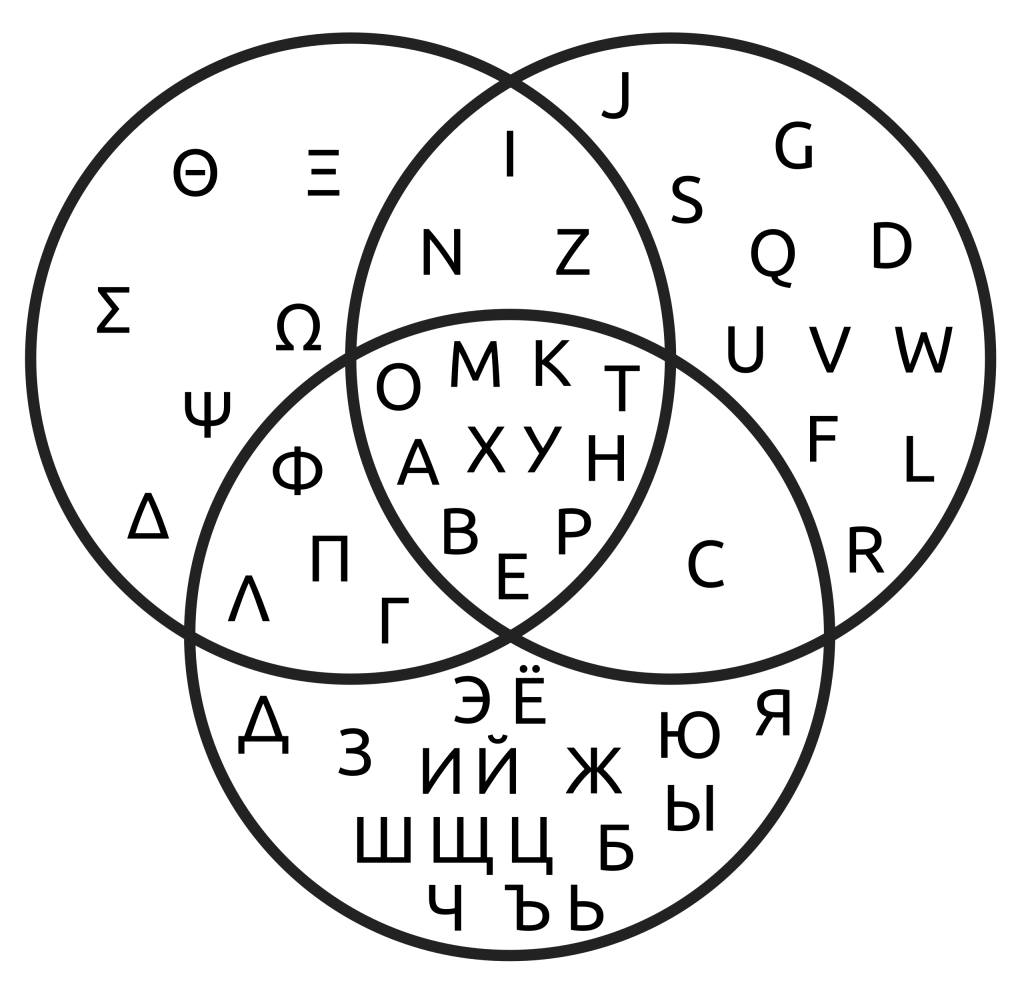
An interesting Venn diagram in Wikipedia  shows the upper-case characters common to the Greek, Latin, and Cyrillic alphabets. As Watchduck happened to size the circles equally, a Reuleaux triangle is their common intersection. ds

© Dennis Simanaitis, SimanaitisSays.com, 2024