DYNAMICAL SYSTEMS THEORY, ANOSOV FLOWS, AND ARNOLD’S CAT PART 2

A FINE ARTICLE IN QUANTA MAGAZINE, Jordana Cepelewicz’s “Flow Proof Helps Mathematicians Find Stability in Chaos,” introduces the concept of Anasov flows in dynamical systems. And, following up with some Internet sleuthing, I came upon Arnold’s cat.

Back when I was reasonably (though not particularly productively) au currant with dynamical systems, the name Vladimir Arnol’d was known to me, at least in part because of the odd apostrophe inserted in the Roman rendering of his Russian surname.

I sense an affinity with this mathematician because of the apparent similarity of his cat to my pal ∏wacket. 

Background on Arnold’s Cat. Wikipedia devotes an entire entry to Arnold’s cat map: “In mathematics, Arnold’s cat map is a chaotic map from the torus into itself, named after Vladimir Arnold, who demonstrated its effects in the 1960s using an image of a cat, hence the name.

Its description is replete with math occasionally having appeared here at SimanaitisSays: “Thinking of the torus 𝕋² as the quotient space ℝ²/ℤ², Arnold’s cat map is the transformation

F: 𝕋² → 𝕋²

given by the formula F(x,y) = (2x+y, x+y) mod 1.

Pithy examples of mathematical notation, these. First, check out the example at Quotient Space of a sphere being the quotient space of a disc. Cool; similarly for a torus (a donut).

Second, the function F maps points into other points by shearing two units to the right, the 2x, x part, and one unit up, the +y parts.

Third, the mod1 jazz shifts the point back into the unit square. See “Arithmetic Can Be Mod”. For instance, clock faces are mod12: Four hours after 11 o’clock is 4 + 11 = 15 = 3 mod12 (the remainder after dividing by 12). 

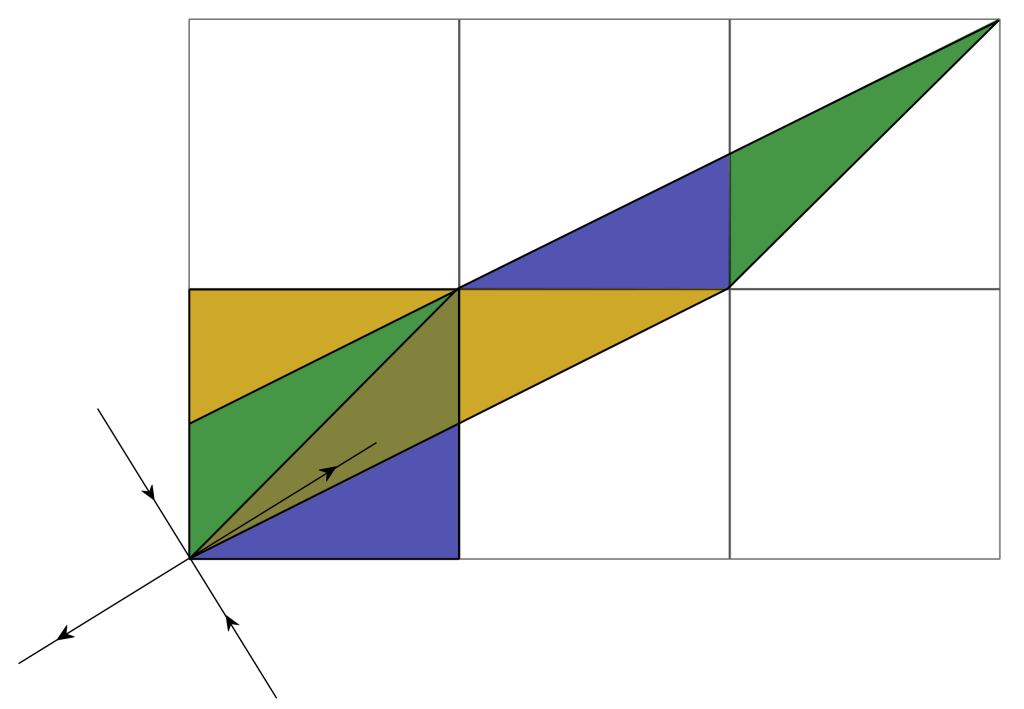
A Repeating Cat. Wikipedia notes that “It is possible to define a discrete analogue of the cat map. One of this map’s features is that image being apparently randomized by the transformation but returning to its original state after a number of steps.”

Wikipedia observes, “The original image of the cat is sheared, and then wrapped around in the first iteration of the transformation. After some iterations, the resulting image appears rather random or disordered, yet after further iterations the image appears to have further order—ghost-like images of the cat, multiple smaller copies arranged in a repeating structure and even upside-down copies of the original image—and ultimately returns to the original image.”

A Pair of Cherries, Similarly Mapped. Check out A Pair of Cherries Undergoing Similar Mappings. I couldn’t find any means of stop-action, and won’t waste your time recounting how many viewings it took to capture the following images.

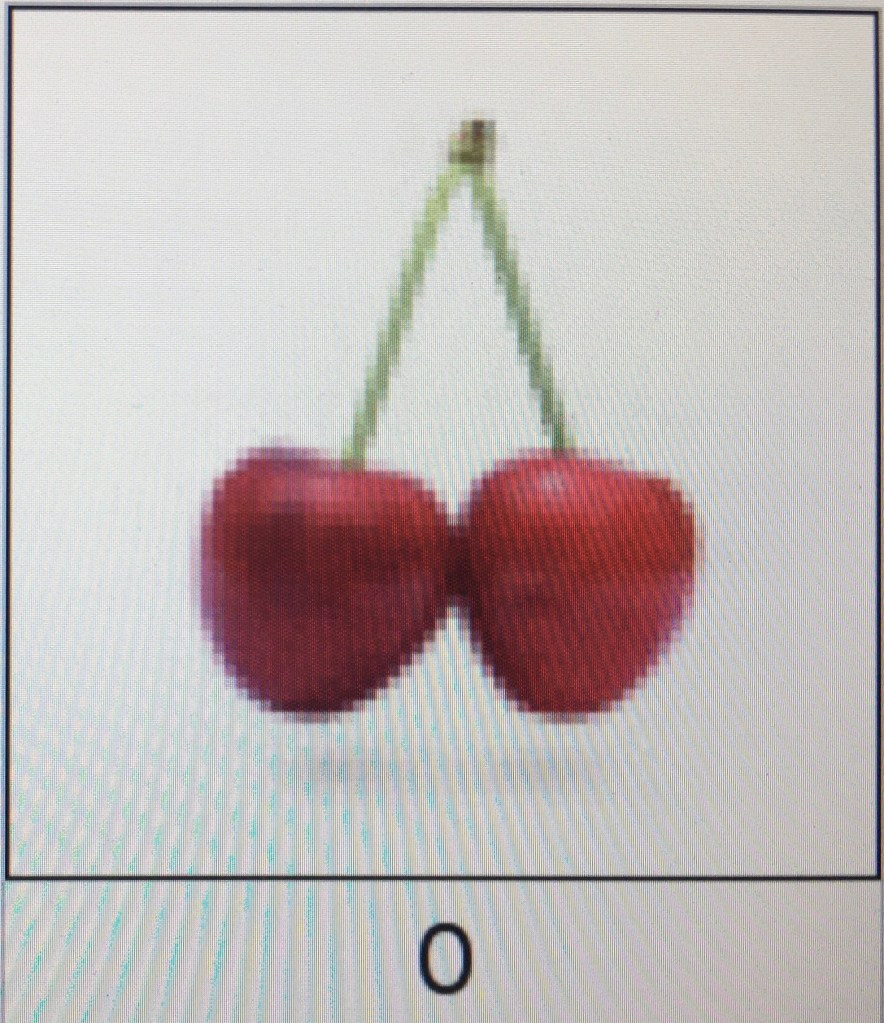
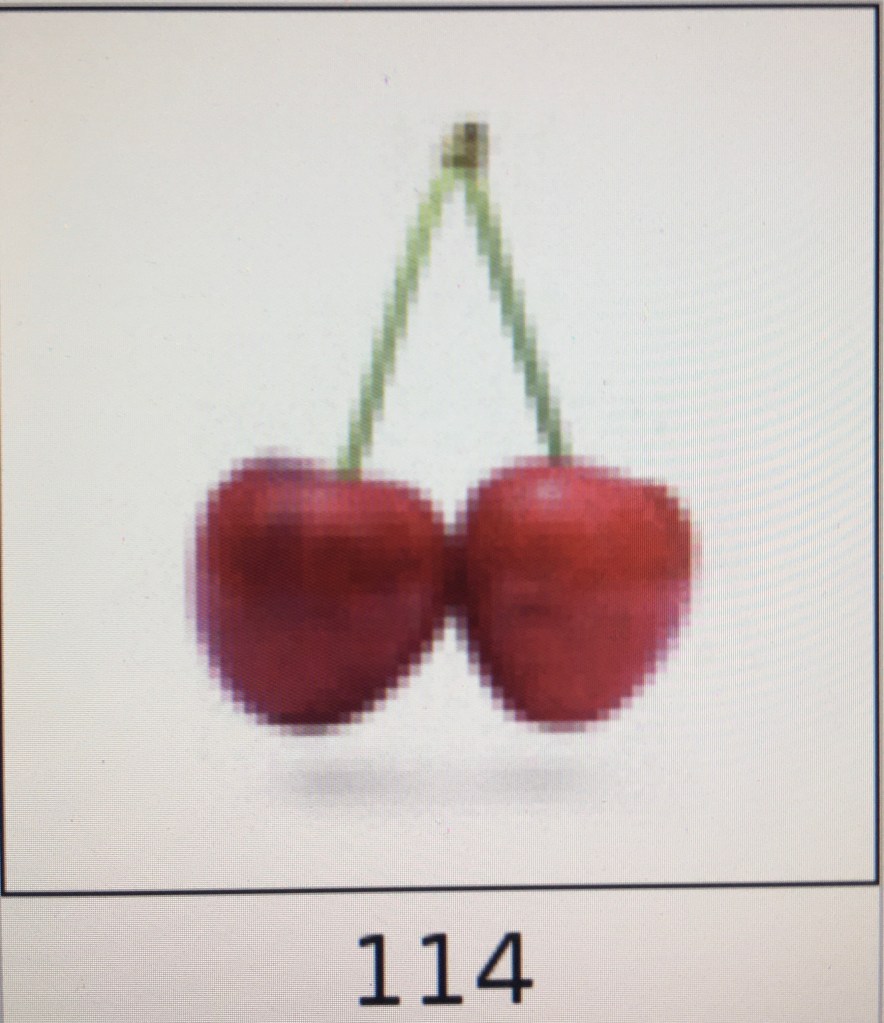
The image is 74 pixels wide, and takes 114 iterations to be restored; it appears upside-down at the 57th iteration. 

All in good fun with dynamical systems theory. ds

© Dennis Simanaitis, SimanatisSays.com, 2023